实例:Tikhonov 正则化模型用于图片去噪
对于真实图片 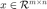 和带噪声的图片
和带噪声的图片 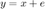 (其中
(其中  是高斯白噪声)。 Tikhonov 正则化模型为:
是高斯白噪声)。 Tikhonov 正则化模型为:
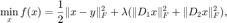
其中 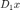 ,
, 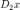 分别表示
分别表示  在水平和竖直方向上的向前差分,
在水平和竖直方向上的向前差分,  为正则化系数。 上述优化问题的目标函数中,第二项要求恢复的
为正则化系数。 上述优化问题的目标函数中,第二项要求恢复的  有较好的光滑性,以达到去噪的目的。 注意到上述目标函数是可微的,我们利用结合BB步长和非精确搜索的 的梯度下降对其进行求解。
有较好的光滑性,以达到去噪的目的。 注意到上述目标函数是可微的,我们利用结合BB步长和非精确搜索的 的梯度下降对其进行求解。
目录
图片和参数准备
设定随机种子。
clear; seed = 97006855; ss = RandStream('mt19937ar','Seed',seed); RandStream.setGlobalStream(ss);
载入未加噪的原图作为参考,记录为 u0 。
u = load ('tower.mat');
u = u.B1;
u = double(u);
[m,n] = size(u);
u0 = u;
生成加噪的图片,噪声  的每个元素服从独立的高斯分布
的每个元素服从独立的高斯分布 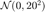 ,并对每个像素进行归一化处理(将像素值转化到[0,1]区间内)。注意到 MATLAB 的 imshow 函数(当第二个参数设定为空矩阵时),能够自动将矩阵中最小的元素对应到黑色,将最大的元素对应为白色。
,并对每个像素进行归一化处理(将像素值转化到[0,1]区间内)。注意到 MATLAB 的 imshow 函数(当第二个参数设定为空矩阵时),能够自动将矩阵中最小的元素对应到黑色,将最大的元素对应为白色。
u = u + 20*randn(m,n); maxu = max(u(:)); minu = min(u(:)); u = (u - minu)/(maxu - minu);
参数设定,以一个结构体提供各参数,分别表示  ,梯度和函数值的停机标准,输出的详细程度,和最大迭代次数。
,梯度和函数值的停机标准,输出的详细程度,和最大迭代次数。
opts = struct(); opts.xtol = 1e-8; opts.gtol = 1e-6; opts.ftol = 1e-16; opts.record = 0; opts.maxit = 200;
求解正则化优化问题
分别取正则化系数为 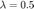 和
和 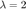 ,利用带BB 步长的梯度下降求解对应的优化问题,见<fminGBB.html 带BB步长线搜索的梯度法> 。
,利用带BB 步长的梯度下降求解对应的优化问题,见<fminGBB.html 带BB步长线搜索的梯度法> 。
lambda = 0.5; fun = @(x) TV(x,u,lambda); [x1,~,out1] = fminGBB(u,fun,opts); lambda = 2; fun = @(x) TV(x,u,lambda); [x2,~,out2] = fminGBB(u,fun,opts);
结果可视化,将不同正则化系数的去噪结果以图片形式展示。
subplot(2,2,1); imshow(u0,[]); title('原图') subplot(2,2,2); imshow(u,[]); title('高斯噪声') subplot(2,2,3); imshow(x1,[]); title('\lambda = 0.5') subplot(2,2,4); imshow(x2,[]); title('\lambda = 2') print(gcf,'-depsc','tv.eps')
Tikhonov 正则化模型的目标函数值和梯度计算
该无约束优化问题的目标函数为:
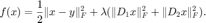
function [f,g] = TV(x,y,lambda)
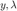 分别表示带噪声图片和正则化参数, f , g 表示在 x 点处的目标函数值和梯度。
分别表示带噪声图片和正则化参数, f , g 表示在 x 点处的目标函数值和梯度。
第一项 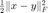 用于控制去噪后的图片
用于控制去噪后的图片  和带噪声的图片
和带噪声的图片  之间的距离。
之间的距离。
f = .5*norm(x - y, 'fro')^2;
计算两个方向上的离散差分, 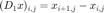 ,
, 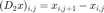 。
。
[m,n] = size(y); dx = zeros(m,n); dy = zeros(m,n); d2x = zeros(m,n); for i = 1:m for j = 1:n ip1 = min(i+1,m); jp1 = min(j+1,n); im1 = max(i-1,1); jm1 = max(j-1,1); dx(i,j) = x(ip1,j) - x(i,j); dy(i,j) = x(i,jp1) - x(i,j);
离散的拉普拉斯算子 d2x : 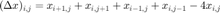 。
。
d2x(i,j) = x(ip1,j) + x(im1,j) + x(i,jp1) + x(i,jm1) - 4*x(i,j);
end
end
计算目标函数的第二项(Tikhonov 正则化)并与第一项合并得到当前点处的目标函数值。
f = f + lambda * (norm(dx,'fro')^2 + norm(dy,'fro')^2);
目标函数的梯度可以解析地写出:

g = x - y - 2*lambda*d2x;
end

结果分析
首先针对图片去噪的效果进行分析。我们发现利用 Tikhonov 正则化模型可以有效地去除图片中的噪声。 当正则化系数  增大时,去噪的效果逐渐增强,但是图片中的物体边界也逐渐模糊。
增大时,去噪的效果逐渐增强,但是图片中的物体边界也逐渐模糊。
同时我们也对带BB 步长的梯度下降法在其中的表现进行分析:在这两个问题中 BB 步长的梯度下降法都以非常迅速地速度收敛到了最优值。当最终收敛时,我们看到梯度的范数 nrmG 已经很小,这表明算法有较好的收敛性。同时注意到,虽然我们采用了回退法的线搜索方法, 但是在上面的应用中 BB 步长总是自然地满足了线搜索准则的要求,因此没有进行额外的步长衰减 (每一步的步长试探次数 ls-Iter 均为1)。
参考页面
在此页面中我们利用梯度法求解模型,算法详见 带BB步长线搜索的梯度法 。
此页面的源代码请见: demo_denoising.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将